Using the Combustion Calculator for HCN, HCl, and Soot

Reading Time: 10 minutes

Created with software version: 2024.1

Download the relevant example files here.

1. Introduction

In a previous tutorial, we described how to use PyroSim to define complex reactions in the Fire Dynamics Simulator (FDS).

You must use complex stoichiometry if:

The fuel does not consist of just \(C\), \(H\), \(N\), \(O\).
To track soot deposition or removal from the atmosphere with HVAC filters.
There are multiple sequential gas phase reactions.

We described several complex stoichiometry examples, but in all cases we simply followed FDS User Guide examples that already provided the complete stoichiometric equation, such as that for PVC (15.2.2 Complex Fuel Molecules, FDS User’s Guide):

\[1\underbrace{\left(C_2 H_3 Cl\right)}_{Fuel} + 1\underbrace{\left(1.53O_2 + 1.53(3.76)N_2\right)}_{Air} \to\]

\[1\underbrace{\left(HCl + H_2 O + 0.14CO + 0.96CO_2 + 0.90C + 1.53(3.76)N_2\right)}_{Products}\]

In this post, we will demonstrate how to use a spreadsheet to calculate the stoichiometric coefficients and then use these calculated coefficients to define the FDS reaction.

In the following discussion, references to FDS are for version FDS-6.9.1-0-g889da6a-release and the corresponding Fire Dynamics Simulator User’s Guide. References to SFPE Handbook are to the SFPE Handbook of Fire Protection Engineering, 5th edition.

2. Background

One piece of information we need is the molecular weights of the species. The FDS User’s Guide provides this information in Table 14.1, a portion of which is shown below in Figure 1.

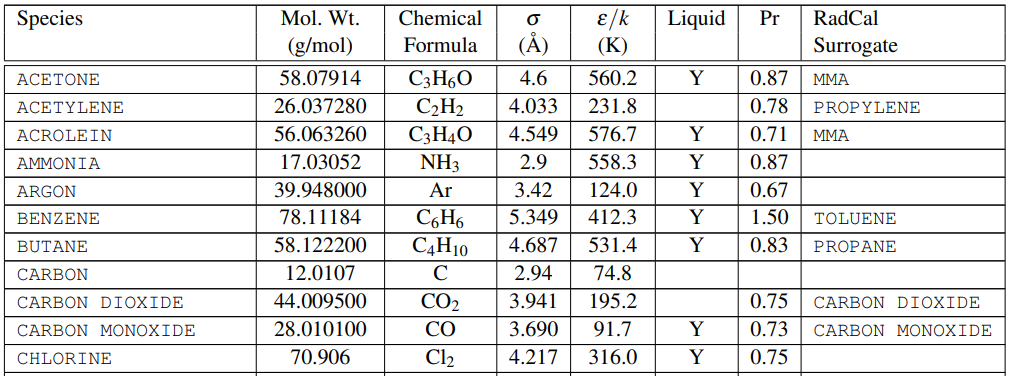
pyro comb calc mol wt — Figure 1. Molecular weights of species from FDS User’s Guide, Table 14.1: Pre-defined gas and liquid species.

We also need the composition of the fuel and products and one source of this information is the SFPE Handbook. Table 36.11, a small portion of which is shown below in (Figure 2), gives the composition of some common polymers and the reaction products. The important information is that the fuels we will work with include \(C\), \(H\), \(O\), \(N\), and \(Cl\). The yields (\(\Psi_{i}\)) include \(CO_{2}\), \(CO\), \(S\), \(HC\), and \(HCl\), where \(S\) is soot.

pyro comb calc fuel table 36 11 2 — Figure 2. Composition of fuel and yields from SFPE Handbook, Table 36.11.

The SFPE Handbook repeats this data in a somewhat different format in Tables 62.17 and 62.18, small portions of which are shown below.

pyro comb calc fuel — Figure 3. Composition of fuel test materials from SFPE Handbook, Table 62.17.

pyro comb calc product 2 — Figure 4. Yields for some common polymeric materials from SFPE Handbook, Table 62.18.

In this post, we base our discussion on examples in the FDS User’s Guide, but if there is interest in examples based on the SFPE data, please contact support@thunderheadeng.com and we can add those.

3. Derivation

We will include \(Cl\) in our fuel, which gives a slightly more general form of the reaction equation given in the FDS User’s Guide, Section 15.1.1.

General Stoichiometric Equation

\[\underbrace{\left(C_{x}H_{y}O_{z}N_{v}Cl_{w}\right)}_{Fuel} \ + \ \underbrace{\left(\nu_{O_{2}}O_{2}\right)}_{Oxygen \ in \ air} \to\]

\[\underbrace{\left(\nu_{CO_{2}}CO_{2} + \nu_{H_{2}O}H_{2}O + \nu_{CO}CO + \nu_{S}Soot + \nu_{HCN}HCN + \nu_{N_{2}}N_{2} + \nu_{HCl}HCl\right)}_{Products}\]

Where \(\nu_{i}\) is the stoichiometric coefficient of the species.

We also assume that the soot has a known volume fraction of hydrogen \(X_{H}\), so the composition is given by:

\[Soot = (1-X_{H})C + X_{H}H\]

Starting with FDS 6.8.0, the default value for soot is \(C\), corresponding to \(X_{H}=0\). In previous versions, the default value for soot hydrogen fraction (SOOT_H_FRACTION) was 0.1, which results in \(Soot = C_{0.9}H_{0.1}\). In these examples we use \(X_{H}=0.1\).

The stoichiometric equation has eight unknown stoichiometric coefficients: \(\nu_{O_{2}}\), \(\nu_{HCl}\), \(\nu_{CO_{2}}\), \(\nu_{CO}\), \(\nu_{S}\), \(\nu_{HCN}\), and \(\nu_{N_{2}}\). But, we have only five independent equations we can write for \(C\), \(H\), \(O\), \(N\), and \(Cl\). We reduce the number of unknowns by specifying yields \(\Psi_{i}\) for \(Soot\), \(CO\), and \(HCN\).

The stoichiometric reaction equation is a simplification of the actual combustion process which can consist of many (maybe hundreds) of intermediate reactions that in turn depend on details of the combustion environment. The yields for \(\Psi_{i}\) for \(Soot\), \(CO\), and \(HCN\) are strongly dependent on whether the combustion is well ventilated or fuel rich, so it is reasonable to use values obtained from experimental data rather than attempt to calculate them rigorously.

The yields are given as fractions of the fuel mass, which we calculate using:

\[W_{Fuel} = x(W_{C}) + y(W_{H}) + z(W_{O}) + v(W_{N}) + w(W_{Cl})\]

The mass of a particular species can be written using either the yield or the stoichiometric coefficient, giving us the following relationship:

\[\nu_{i}= \frac{W_{Fuel}}{W_{i}}\Psi_{i}\]

Thus, we can immediately calculate the stoichiometric coefficients \(\Psi_{i}\) for \(Soot\), \(CO\), and \(HCN\).

We substitute the known stoichiometric coefficients into the general reaction equation and rearrange with unknown terms on the left and known terms on the right.

\[\nu_{HCl}HCl + \nu_{CO_{2}}CO_{2} + \nu_{H_{2}O}H_{2}O + \nu_{N_{2}}N_{2} - \nu_{O_{2}}O_{2} =\]

\[C_{x}H_{y}O_{z}N_{v}Cl_{w} - \nu_{CO}CO - \nu_{S}(X_{H}H + (1 - X_{H})C) - \nu_{HCN}HCN\]

Now we write separate equations to balance \(C\), \(H\), \(O\), \(N\), and \(Cl\). For example, balancing \(C\) gives us:

\[\nu_{CO_{2}} = x - \nu_{CO} - \nu_{S}(1 - X_{H}) - \nu_{HCN}\]

And balancing \(H\) gives us:

\[\nu_{HCl} + 2\nu_{H_{2}O} = y - \nu_{S}X_{H} - \nu_{HCN}\]

Arranging the equations in matrix form, we obtain:

\[\begin{bmatrix}1 & 0 & 0 & 0 & 0 \\0 & 2 & 0 & 0 & 1 \\2 & 1 & 0 & -2 & 0 \\0 & 0 & 2 & 0 & 0 \\0 & 0 & 0 & 0 & 1 \end{bmatrix}\left(\begin{array}{c}\nu_{CO_{2}}\\ \nu_{H_{2}O}\\ \nu_{N_{2}}\\ \nu_{O_{2}}\\ \nu_{HCl}\end{array}\right) = \left(\begin{array}{c}x-\nu_{CO}-\nu_{S}(1-X_{H})-\nu_{HCN}\\ y-\nu_{S}X_{H}-\nu_{HCN} \\ z-\nu_{CO} \\v-\nu_{HCN} \\w\end{array}\right)\]

We can now solve for our unknown stoichiometric coefficients.

This is not the only way to approach this problem, but it is a simple method that can always be applied to other cases.

4. Spreadsheet Implementation

Download the spreadsheet that implements these calculations through the link at the top of this tutorial.

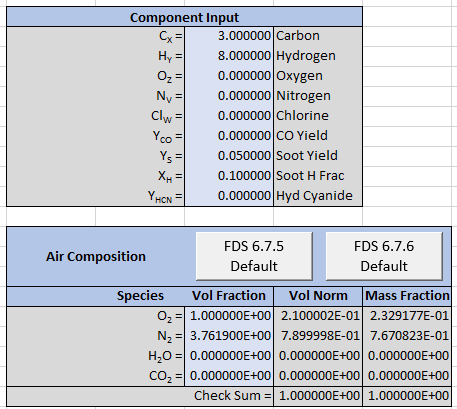
User input to describe the reaction consists of the fuel composition (\(x\), \(y\), \(z\), \(v\), and \(w\)), the known yields of product (\(\Psi_{CO}\), \(\Psi_{Soot}\), and \(\Psi_{HCN}\)), and the hydrogen fraction of soot (\(X_{H}\)).

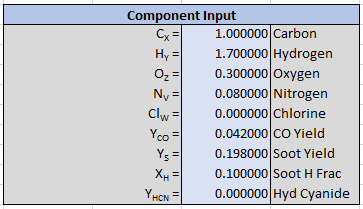
pyro comb spreadsheet input reaction — Figure 5. Reaction input to the combustion calculator.

Only the oxygen in the air is used in the reaction calculation, but the user can specify the complete composition of the air. Air species will then be included in the calculation of products.

pyro comb spreadsheet input air — Figure 6. Air composition - Air can be simplified, for example to include only \(O_{2}\) and \(N_{2}\).

The output is given in a form that can be used to specify a complex reaction in FDS.

\[C_{1}\ Fuel + C_{2}\ Air \to C_{3}\ Products\]

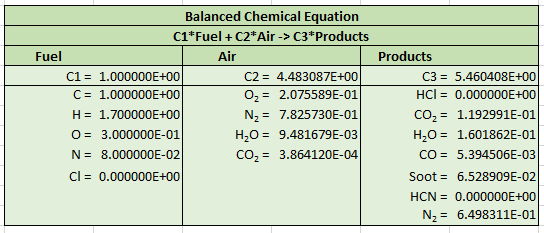
pyro comb spreadsheet output — Figure 7. Combustion calculator output.

We also provide the output reformulated with soot as a separate product species. This is useful if the user is calculating soot deposition of filtration.

Although not related to the reaction balance, the heat of combustion is also calculated using the energy released per unit mass of oxygen consumed. The user can specify the desired heat release rate and the corresponding mass fuel flow rate will be calculated.

5. Examples

5.1. Combustion of Polyvinyl Chloride (PVC)

5.1.1. Spreadsheet Calculation

This example demonstrates combustion of PVC and is described in Section 15.2.2 Complex Fuel Molecules of the FDS User’s Guide.

"For example, chlorine is commonly found in building and household materials, and because of its propensity to form the acid gas \(HCl\), you may want to account for it in the basic reaction scheme. Suppose the predominant fuel in the fire is polyvinyl chloride (PVC). Regardless of its detailed polymeric structure, it can be regarded as \(C_{2}H_{3}Cl\) for the purpose of modeling. Assuming that all of the \(Cl\) in the fuel is converted into \(HCl\), you can derive a single-step reaction mechanism using appropriate \(Soot\) and \(CO\) yields for the specified fuel."

The chemical reaction from the FDS User’s Guide is:

\[1(C_2 H_3 Cl) + 1(1.53O_2 + 1.53(3.76)N_2) \to\]

\[1(HCl + H_2 O + 0.14CO + 0.96CO_2 + 0.90C + 1.53(3.76)N_2)\]

A corresponding FDS input file pvc_combustion.fds included in the download for this tutorial, and is an FDS Species Verification example. The reaction input from this file is shown below.

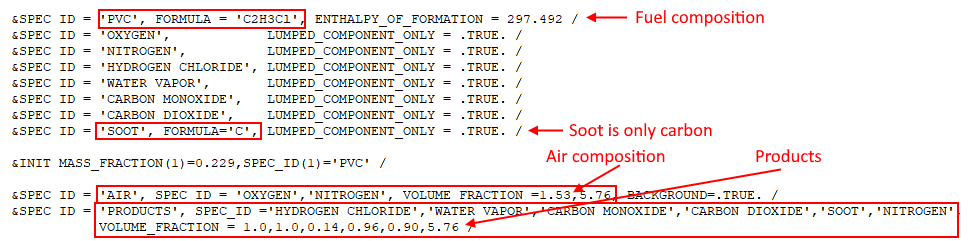
pyro comb calc fds input annotated — Figure 8. The FDS pvc_combustion.fds input file.

In this example, air has been simplified to consist only of \(O_{2}\) and \(N_{2}\). Also note the slight difference in \(N_{2}\) given in the combustion equation (\(1.53(3.76) = 5.7528\)) and in the input file (\(5.76\)).

The FDS User’s Guide description states the Soot and CO yields are 0.172 and 0.063, but because we want to replicate the reaction exactly we must use more significant figures. We calculate the yields from the given product stoichiometric coefficients. In this example, the hydrogen fraction of soot is zero so the \(Soot\) stoichiometric coefficent of 0.9 gives us a yield \(\Psi_{Soot} = 0.172959\) and the \(CO\) coefficient of 0.14 gives us \(\Psi_{CO} = 0.0627444\).

The input to the spreadsheet is shown below.

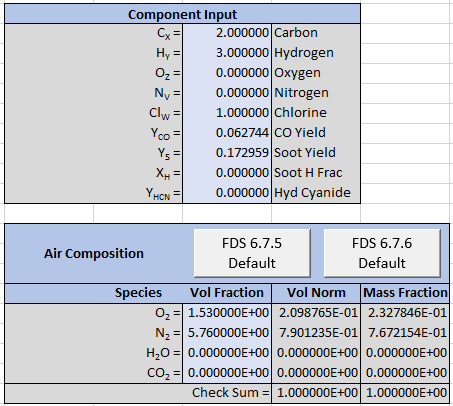
pyro comb calc pvc spreadsheet input — Figure 9. Spreadsheet input for PVC calculation

And this is the corresponding output.

pyro comb calc pvc spreadsheet output — Figure 10. Spreadsheet output for PVC calculation

In the spreadsheet we normalize the Air and Products components to make it easier to compare with the *.out file data. So the spreadsheet results are written as:

\[1(C_2 H_3 Cl) + 7.29(0.2098765O_2 + 0.7901235N_2) \to\]

\[9.76(0.1024590HCl + 0.1024590H_{2}O + 0.01434426CO + 0.09836066CO_2 + 0.09221311Soot + 0.5901639N_2)\]

Which is equivalent to the input from the FDS example file as shown in Figure 8.

5.1.2. Comparing to FDS Output

FDS provides details of the species compositions and reaction calculations in the *.out file. We will show how to compare the FDS output with the spreadsheet calculation.

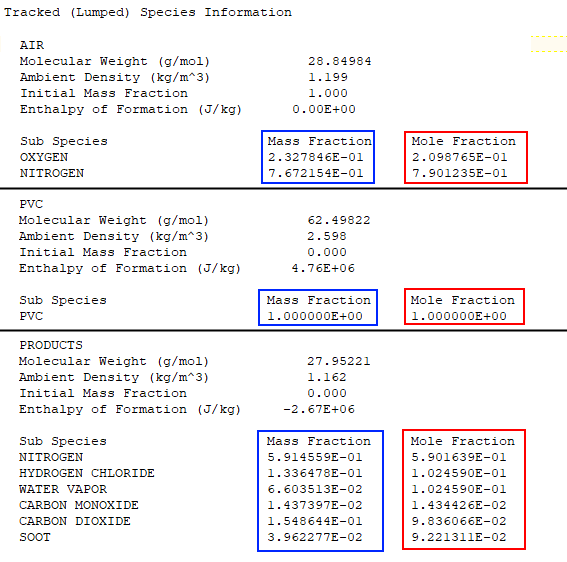
As we scroll through the *.out file, we see the Mass Fraction Transformation Matrix followed by the Primitive Species Information. Next we find the Tracked (Lumped) Species Information, as shown below. The mole fractions of the tracked species are directly comparable to the values shown in Figure 10. Similarly, the mass fractions can be compared to the Combustion Process table in the spreadsheet (not shown).

pyro comb fds out 1 — Figure 11. FDS species and reaction output in *.out file

Scrolling further down in the *.out file we find the Gas Phase Reaction Information. The molar coefficients correspond to C1, C2, and C3 in Figure 10.

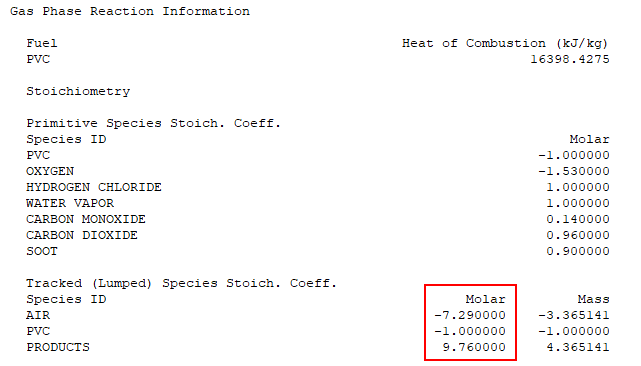
pyro comb fds out 2 — Figure 12. FDS reaction coefficients in *.out file

We have verified that the spreadsheet calculations match the FDS reaction calculations. The user should always review the reaction information when performing a simulation.

A PyroSim model of this example was made using the steps described in the Complex Stoichiometry Post and is included in the download files here.

5.2. Combustion of Polyisocyanurate

This example uses polyisocyanurate which produces hydrogen cyanide (HCN).

A corresponding FDS input file FED_CO_HCN.fds included in the download for this tutorial, and is an FDS Species Verification example. A PyroSim model of this example is also included in the download files.

The reaction parameters from the input file are:

pyro comb calc fds input hcn — Figure 13. FDS combustion of Polyisocyanurate.

The corresponding spreadsheet input is:

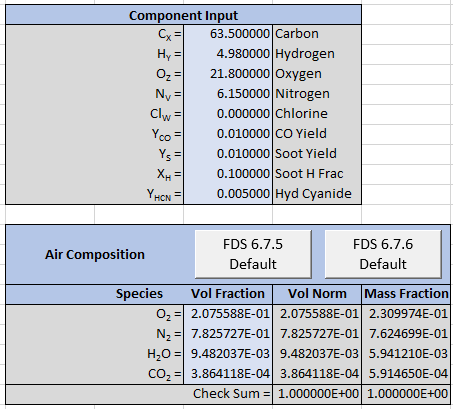
pyro comb spreadsheet input hcn — Figure 14. Combustion of Polyisocyanurate Spreadsheet Input.

The spreadsheet output is shown below. We can again compare to FDS output and the results are identical.

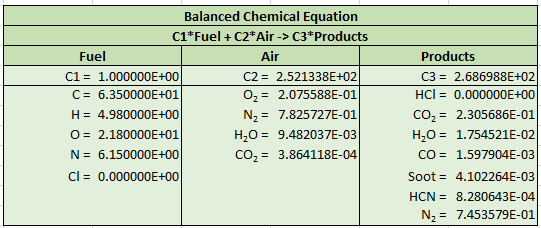
pyro comb spreadsheet output hcn — Figure 15. Combustion of Polyisocyanurate Spreadsheet Output.

5.3. Soot deposition

The spreadsheet can also be used for soot deposition or HVAC filtration problems such as described in the Complex Stoichiometry Post.

The example is from the FDS User’s Guide, 15.4.1 Example Case: Soot Deposition from a Propane Flame.

A corresponding FDS input file propane_flame_deposition.fds included in the download for this tutorial, and is an FDS Aerosols Verification example. A PyroSim model of this example is also included in the download files.

The stoichiometric equation is:

\[1\underbrace{\left(C_3 H_8\right)}_{Fuel} + 4.81308\underbrace{\left(O_2 + 3.7619N_2\right)}_{Air} \to\]

\[1\underbrace{\left(18.10631N_2 + 2.81813CO_2 + 3.98990H_2 O \right)}_{Products} + 0.20201\underbrace{\left(C_{0.9} H_{0.1}\right)}_{Soot}\]

The spreadsheet input is shown below.

pyro comb spreadsheet input soot — Figure 16. Depostion of Soot.

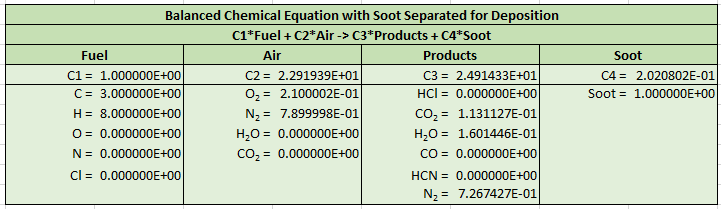
The output is reformatted so that Soot is now a separate product and the stoichiometric equation is now given by:

\[C_{1}\ Fuel + C_{2}\ Air \to C_{3}\ Products + C_{4}\ Soot\]

The example PyroSim model shows how to define the normalized lumped species of air and products. The default SOOT species is used and the corresponding reaction coefficients are the constants \(C_{2}\), \(C_{3}\), and \(C_{4}\). Comparison with the FDS example show that the reactions are identical.

pyro comb spreadsheet output soot — Figure 17. Depostion of Soot calculated stoichiometric equation.

6. Closing

To download the most recent version of PyroSim, please visit the PyroSim Support page and click the button for the current release.

If you have any questions, please contact support@thunderheadeng.com

Using the Combustion Calculator for HCN, HCl, and Soot

Related Tutorials